立体几何在高中阶段属于中档难度的知识点，在高考数学中占22分，每年高考雷打不动，一道大题12分，和一道选择题5分，这个分值比例是很高的。尤其是立体几何证明题目的考查，更是对同学们逻辑论证能力的考验。北京高考在线建议想要在立体几何上拿高分，就要知道立体几何的解题技巧和题型考法，因为任何题型的解题都是有方法的，同学们不要盲目去学，不要盲目去做题，吃透题型，那么高考分数自然就高。

点此查看>>>2024年北京高考各科目知识点汇总

一、平行垂直位置关系的论证

（1）由已知想性质，由求证想判定，即分析法与综合法相结合寻找证题思路。

（2）利用题设条件的性质适当添加辅助线（或面）是解题的常用方法之一。

（3）三垂线定理及其逆定理在高考题中使用的频率最高，在证明线线垂直时应优先考虑。

二、空间角的计算方法与技巧

（1）两条异面直线所成的角①平移法：②补形法：③向量法：

（2）直线和平面所成的角①作出直线和平面所成的角，关键是作垂线，找射影转化到同一三角形中计算，或用向量计算。②用公式计算。

（3）二面角①平面角的作法：（i）定义法；（ii）三垂线定理及其逆定理法；（iii）垂面法。②平面角的计算法：（i）找到平面角，然后在三角形中计算（解三角形）或用向量计算；（ii）射影面积法；（iii）向量夹角公式。

三、空间距离的计算方法与技巧

（1）求点到直线的距离：经常应用三垂线定理作出点到直线的垂线，然后在相关的三角形中求解，也可以借助于面积相等求出点到直线的距离。

（2）求两条异面直线间距离：一般先找出其公垂线，然后求其公垂线段的长。在不能直接作出公垂线的情况下，可转化为线面距离求解（这种情况高考不做要求）。

（3）求点到平面的距离：一般找出（或作出）过此点与已知平面垂直的平面，利用面面垂直的性质过该点作出平面的垂线，进而计算；也可以利用“三棱锥体积法”直接求距离；

四、几平面图形的翻折、立体图形的展开等一系列问题

要注意翻折前、展开前后有关几何元素的“不变性”与“不变量”。

五、与球有关的题型

只能应用“老方法”，求出球的半径即可。

六、经典例题分析

例1．在正三棱锥S－ABC中，E为SA的中点，F为△ABC的中心

，SA=BC=2，则异面直线EF与AB所成的角是（ ）

（A）30° （B） 45° （C） 60° （D） 90°

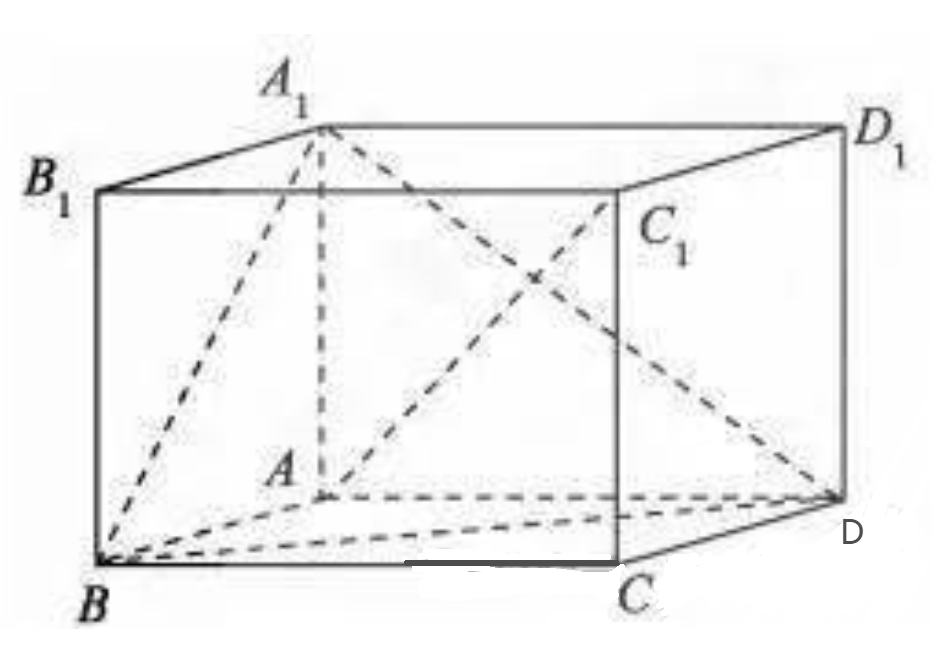
例2．如图，在平行六面体ABCD-A1B1C1D1中，AA1⊥平面ABCD，且AB=AD=2，AA1=根号3，∠BAD=120.（1）求异面直线A1B与AC1所成角的余弦值；

声明：本文由北京高考在线团队（微信公众号：bjgkzx）排版编辑，内容来源于网络整理，如有侵权，请及时联系管理员删除。